Let y = m1x + c1 and y = m2x + c2 be the equations of two lines in a plane where,
m1 = slope of line 1 c1 = y-intercept made by line 1 m2 = slope of line 2 c2 = y-intercept made by line 2

<BAX = θ1 <DCX = θ2 ∴ m1 = tan θ1 and m2 = tan θ2
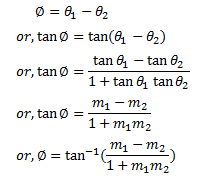
Also if we consider <APD as the angle between lines,

Hence, the angle between two lines is,
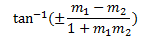
Condition for perpendicularity
The two lines are perpendicular means. Ø = 90°

Thus, the lines are perpendicular if the product of their slope is -1.
Condition for parallelism
The two lines are perpendicular means, Ø = 0°

Thus, the lines are parallel if their slopes are equal.
Angle Between Two Lines Examples
1. Find the angle between the lines 2x-3y+7 = 0 and 7x+4y-9 = 0.
Solution:
Comparing the equation with equation of straight line, y = mx + c,
Slope of line 2x-3y+7=0 is (m1) = 2/3
Slope of line 7x+4y-9=0 is (m2) = -7/4
Let, Ø be the angle between two lines, then

2. Find the equation of line through point (3,2) and making angle 45° with the line x-2y = 3.
Solution:
Let m be the slope of the required line passing through (3,2). So, using slope point form, its equation is
y-2 = m(x-3) ——— (i)
Slope of line x-2y = 3 is 1/2.
Since, these lines make an angle of 45° so,

Substituting values of m in equation (i), we get
y-2 = 3(x-3) and y-2 = -(x-3)/3
or, 3x-y-7 = 0 and x+3y-9 = 0 are the required equations of line.